Magnitud

Es todo aquello que se puede medir, que se puede representar por un número y que puede ser estudiada en las ciencias experimentales (que observan, miden, representan....).
Ejemplos de magnitudes: velocidad, fuerza, temperatura, energía física (no la energía espiritual?), etc.

Para obtener el número que representa a la magnitud debemos escoger una cantidad de esa magnitud que tomamos como unidad.
Para medir la masa, por ejemplo, tomamos (más o menos arbitrariamente) como unidad una cantidad materia a la que llamamos kg.
Las unidades deben ser:

1. reproducibles: por cualquiera y no manipulables por el poder (que nadie varíe de manera localista lo que corresponde a un mismo nombre: libra de Roma y libra de Florencia)
   La idea de como deben ser las unidades, surge como una consecuencia de la Revolución Francesa.
2. inalterables: por las condiciones atmosféricas, el uso, etc.
3. universales y contrastables: utlizables por todos los paises y accesibles para calibrar frenete a ellas otros patroneszables por todos los paises y accesibles para calibrar frenete a ellas otros patrones

La Medida es el resultado de medir, es decir, de comparar la cantidad de magnitud que queremos medir con la unidad de esa magnitud. Este resultado se expresará mediante un número seguido de la unidad que hemos utilizado: 4m, 200 Km , 5 Kg, etc.

Ejemplo: Calcula el número de cifra significativas de una medida que se expresa como: 4,563 ± 0,02

Analizando como la imprecisión (0,02) nos indica la certeza de conocimineto de los distintos digitos tenemos:

Por lo tanto sabemos que la medida tiene tres cifras significativas: las dos primeras se conocen con certeza total y en la tercera (el 6) tenemos una cierta incertidumbre, pero también es significativa.
La expresión correcta de la medida debe ser 4,56 ± 0,02

Regla para establecer las cifras significativas:

1. La primera cifra de la izquierda distinta de cero, es la cifra más significativa.
2. Si no hay coma decimal, la última cifra de la derecha distinta de cero es la menos significativa.
3. Si hay coma decimal, la última cifra de la derecha aunque sea cero es la menos significativa.
4. Son cifras significativas todas las que se encuentran entre la más y la menos significativa.

Ejemplos:

Son los que se repiten constantemente y afectan al resultado en un sólo sentido (aumentando o disminuyendo la medida).
Pueden ser debidos a un mal calibrado del aparato, a la utilizacion de fórmulas (teoría) incorrectas, al manejo del aparato de forma no recomendada por el fabricante, etc. Estos errores sólo se eliminan mediante un análisis del problema y una "auditoría" de un técnico más cualificado que detecte lo erróneo del procedimiento.

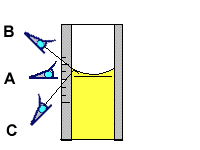La lectura correcta es la efectuada desde A. Cuando mires desde arriba o desde abajo, no enfilas el menisco (curvatura del líquido) y además el nivel te parecera estar en otra división

Ea = imprecisión = incertidumbre

El error absoluto indica el grado de aproximación y da un indicio de la calidad de la medida. El conocimiento de la calidad se complementa con el error relativo.

Se puede dar en % de error relativo. En efecto, si cometemos un error absoluto de un metro al medir la longitud de un estadio de fútbol de 100 m y también un metro al medir la distancia Santiago-Madrid, de aproximadamente 600.000 m, el error relativo será 1/100 (1%) para la medida del estadio y 1 /600.000 para la distancia Santiago-Madrid. Tiene mucha más calidad la segunda medida.

El "medidor" (observador) puede originar errores sitemáticos por una forma inadecuada de medir, introduciendo así un error siempre en el mismo sentido. No suele ser consciente de cómo introduce su error. Sólo se elimina cambiando de observador.
El observador puede introducir también errores accidentales por una imperfección de sus sentidos. Estos errores van unas veces en un sentido y otros en otro y se pueden compensar haciendo varias medidas y promediándolas.

La temperatura, la presión, la humedad, etc pueden alterar el proceso de medida si varían de unas medidas a otras. Es necesario fijar las condiciones externas e indicar, en medidas precisas, cuales fueron éstas. Si las condiciones externas varían aleatoriamente durante la medida, unos datos pueden compensar a los otros y el error accidental que introducen puede ser eliminado hallando la media de todos ellos.

A menudo usamos números con muchos ceros (muy grandes o muy pequeños) que pueden escribirse abreviadamente usando potencias de 10. Esto permite tener idea del orden de magnitud con una simple ojeada, operar más fácilmente e incluso revisar rápidamente operaciones realizadas con ellos.

Utilizando la notación científica el número se escribe como el producto de dos partes: un número comprendido entre 1 y 10 y una potencia de 10. El número se representa con una cifra entera seguida de todas las cifras significativas y multiplicado por la potencia de 10 que corresponda para lograr la equivalencia.

Ej: 0,0001230=1,230· 10 ^-4

120000000=1,2·10 ⁸

En los cálculos aproximados y en descripciones generales, como cuando decimos: "es una distancia de .... km", se suele expresar la cantidad por su orden de magnitud, para lo cual se toma por redondeo la potencia de 10 más próxima al número.

Ejemplos:

Los instrumentos de medida pueden introducir un error sistemático en el proceso de medida por un defecto de construcción o de calibración. Sólo se elimina el error cambiando de aparato o calibrándolo bien.
Debemos conocer el rango de medida del aparato, es decir, entre que valores, máximo y mínimo, puede medir. Uno es la cota máxima y otro la cota mínima.
Los instrumentos deben indicar el límite de protección (por ejemplo un amperímetro que tenga una protección frente a corrientes de hasta 1 A mediante un fusible).

Deben tener las siguientes cualidades :

Rapidez

Es rápido si necesita poco tiempo para su calibración antes de empezar a medir y si la aguja o cursor alcanza pronto el reposo frente a un valor de la escala cuando lanzamos la medida. La aguja no oscila mucho tiempo.

Sensibilidad
Es tanto más sensible cuanto más pequeña sea la cantidad que puede medir. Una balanza que aprecia mg es más sensible que otra que aprecia gramos.
Umbral de sensibilidad es la menor división de la escala del aparato de medida
La sensibilidad con que se fabrican los aparatos de medida depende de los fines a los que se destina. No tendría sentido fabricar una balanza que aprecie mg para usarla como balanza de un panadero.

Fidelidad
Un aparato es fiel si reproduce siempre el mismo valor, o valores muy próximos, cuando medimos la misma cantidad de una magnitud en las mismas condiciones.
Es fiel si la aguja se coloca en el mismo punto de la escala -o muy próximo- cuando repetimos la medida con la misma cantidad de magnitud.
Es fiel si dispersa poco las medidas.

Precisión
Un aparato es preciso si los errores absolutos (desviación de lo que mide del "valor verdadero") que se producen al usarlo son mínimos. El valor que da en cada medida se desvía poco del "valor verdadero".
Un aparato es preciso si es muy sensible y además es fiel (produce poca dispersión de las medidas). Naturalmente debe estar previamente bien calibrado.
Es muy preciso si da poca imprecisión.
La precisón de un aparato analógico electrónico (voltímetro, etc) la indica el fabricante para cada rango de medida.
La precisión define la "clase del instrumento" y está indicada en error relativo absoluto (porcentual absoluto) referido al valor máximo de la escala y especificado para cada rango o escala.
El error absoluto máximo de una medida en esa escala se halla aplicando el error relativo al valor del fondo de escala

Ejemplo: Para un voltímetro "clase 2" en la escala de rango 0-250 V el fabricante asegura una Precisión porcentual absoluta del 2%. Por lo tanto el Error absoluto en esa escala será = 2% . 250 = ± 5V.
En una medida de 230 V tendremos una imprecisión de ± 5V. El mismo que tendremos en una medida de 20 V en esa escala (o sea, ±5V)
Por lo tanto el error relativo (porcentual relativo) es mucho mayor en la parte baja de la escala: 5 / 20, frente a 5 / 230 en la alta.

¡Por esto debes cambiar de escala, para poder hacer las lecturas en la parte alta!

En este polímetro la sensibilidad del aparato (la menor división) en esa escala 0-250 es 5V ( ver la figura anterior arriba) y coincide con la precisón.
La precisión del aparato influye en la precisión con que podemos expresar el resultado de la medida.

Precisión al realizar varias medidas:
Si debemos repetir las medidas, influye en la precisón de todas ellas otra cualidad del aparato: la fidelidad.

Ejemplo: Si relizamos 5 medidas con dos balanzas de la misma sensibilidad, que aprecian cg por ejemplo, será más precisa la que dé menor dispersión de medidas.

Las dos balanzas dan como medida 25,55 g (media aritmética) pero la precisión de la primera es mayor y nos asegura que el valor verdadero está comprendido entre 25,54 g y 25,56 g. La otra balanza nos lo asegura entre 25,52 g y 25,58 g.

La que da las medidas con menor imprecisión es la más precisa.

Ejemplos de instrumentos poco precisos:

Ejemplos de instrumentos de poca precisión son una balanza de cocina y la cinta de modista (muy elastica y que se deforma por el uso). Fíjate en las indicaciones de la escala de esta balanza de cocina.

Toma una cinta muy usada y mide con ella una distancia de 25 cm. Mide la misma distancia con una regla.